As you walk through the endless maze that is Wuse Market, Abuja, you try your best to ignore everyone, as you search for the bookstore that has the entire Harry Potter collection. To your right, a plethora of Igbo traders mercilessly twist their shoes and belts. A group of Hausa jewellers call out to you, presumably to come check out their gold wares. Mama Mimi won’t stop gesticulating to you, to come try today’s iteration of her trademark Rock Buns, but thanks to your new noise cancelling headphones, all you hear is James Blake, crooning his version of “A Case Of You”.
So how exactly do these cans work? To understand, we’d have to make a distinction between Passive and Active noise cancellation. Let’s start with passive. Passive noise cancelling headphones work by physically covering the ears, with leather and foam to help block out external noises, and keep in as much of the music as they can.
Now, active cans are where the magic happens, but first, let’s talk about what sound is. All sound is created by changes in air pressure – vibration. Objects vibrate, and then cause the air around them to vibrate. The faster this vibration (frequency) is, the higher the sound’s pitch, and the taller the wave is (amplitude), the louder it is. Easiest way to represent this is a sine wave.
Enter Fourier Theorem
I’m going to try to skip all the boring math.
Around 1822, French mathematician, Jean-Baptiste Joseph Fourier created the eponymous theorem, which implies that all sounds, no matter how complex, can be represented as a series of sine waves.
What does this have to do with noise cancellation?
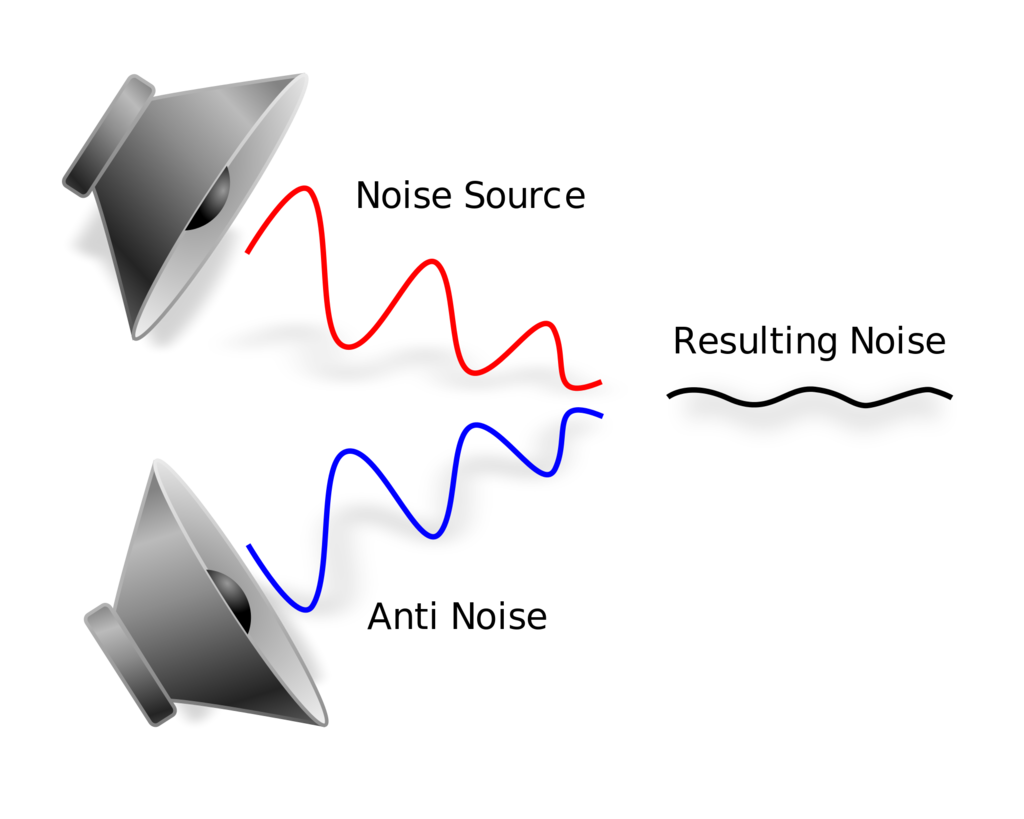
Active noise cancelling headphones all have a small microphone that captures all the ambient sound around you, and uses the Fourier Transform equation to separate the complex sounds into the sine waves that make them up, and then generates a wave that is 180 degrees out of phase (anti-wave) with the ambient noise, effectively cancelling it. This process is called Phase Cancellation.
To make things simpler, think of any number, say 13. How do we get 13 to turn to 0? By subtracting 13 from it. So, we have one wave [13], and we add an opposite wave with equal power [-13], and we have [13 + (-13) = 0]. By constantly taking in sound from your surroundings, and generating the opposite sound, active cans are able to reduce the noise to the barest minimum.
So, thanks to Joseph Fourier, I can enjoy music in the market without hearing shouts of “brother, I get your size”.
Thanks, Fourier.
Photo Credit: tom_bullock, Wikipedia via Compfight cc